알고리즘 ch13 NP-complete Problems
Optimization problem : 최적의 답를 찾는 문제 ex) shortest path
Decision problem : 답이 yes or no 인 문제
Class P
- 어떤 decision 문제에 대해 polynomial time에 그 문제에 대한 해결법을 찾아낼 수 있다면, 그 문제는 클래스 P에 속한다.
즉, 다항시간내에 풀 수 있는 decision 문제들의 class를 class P라고 한다.
다항시간(polynomial time) : O(n^k)
다항시간내에 풀 수 있는 문제들은 tractable하다고 한다.
문제의 어떤 알고리즘이 다항시간내에 풀린다면 efficient 알고리즘이라고 한다.
Class NP
- 어떤 문제가 non-deterministic polynomial time algorithm이 존재한다면 그 문제는 클래스 NP에 속한다.
즉, 어떤 certificate가 다항시간에 문제를 verify할 수 있다면 그 문제는 클래스 NP에 속한다.
상관관계를 생각해보면.
polynomial time algorithm이 존재하는 문제들 즉 class P에 속하는 문제들은 모두 class NP에 속한다.
=> P ⊂ NP
NP example
Problem : 그래프 내에 가중치가 K이하인 MST가 존재하는가?
Verification Algorithm:
1. 하나의 Certificate를 사용한다. (vertex가 n개라고 할때)
2. certificate가 spanning tree를 형성하는지 확인(포함된 vertex가 n개, edge가 n-1개 인지) // O(n)
3. certificate의 가중치의 합이 K를 넘지않는지 확인 // O(m)
Analysis : 증명과정에서 O(n+m)시간 걸림 즉, 이 문제에 대한 certificate 증명이 다항시간에 수행됨
따라서 이 문제는 Class NP에 속함.
Class NP-hard
- NP class에 있는 모든 문제가 어떤 문제(Q)로 reducible할 수 있다면 그 문제(Q)는 클래스 NP-hard에 속한다.
즉, 문제 Q를 풀면 NP class의 모든 문제를 풀 수 있다.
문제 Q는 NP class의 모든 문제들보다 쉽지 않다. => 어렵거나 같다.
(예를 들어)
A라는 문제는 n개의 원소를 정렬하는 문제라 하고
B라는 문제는 n개의 원소에서 가장 큰 값을 찾는 문제라고 하자.
A문제를 푸는 알고리즘으로 B를 풀 수 있다. 이럴 때 문제 B를 문제 A로 reduction(환원) 가능하다고 한다.
따라서 문제 A는 문제 B보다 어렵다.
Class NP-complete
- NP-hard에도 포함되고 NP에도 포함되는 문제는 클래스 NP-complete에 속한다.
- NP-complete 문제들
1. Circuit-sat : circuit analogue of SAT.
2. sat : boolean sanctification problem이라고도 한다.
어떠한 변수들로 이루어진 논리식이 주어졌을 때, 그 논리식이 참이 되는 변수값이 존재하는지를 찾는 문제
[예제] (a+b+d)(¬a+¬c)(¬b+c+¬d+e) 논리식이 있을 때 이 논리식이 1이 나오게하는 a,b,c,,,값이 있느냐
+는 or연산이고, ()는 and연산, ¬는 not연산이다.
literal은 a,b,..같은 것들을 뜻하고 clause는 () 하나를 뜻한다.
예를 들어 3-SAT는 한 절에 들어가는 리터럴 개수를 3개 이하로 제한하는 문제이다.
reduction from Circuit-sat
3. Vertex-cover : 주어진 그래프 G=(V,E) 에서 많아야 K개의 정점을 사용해서 모든 edge를 cover할 수 있는가
reduction from 3sat
4. Set-cover : 주어진 집합 S = {1, 2, 3, …, n}에 대해서 S의 부분집합들이 주어질 때,
이 부분 집합들 중에서 합집합하여 S와 같게 되는 부분 집합들을 집합 커버라고 한다.
집합 커버 문제는 가장 적은 수의 부분 집합으로 이루어진 집합 커버를 찾는 문제
reduction from Vertex-cover = set-cover를 풀면 vertex-cover 풀수있음
5. Subset-sum : 주어진 정수 집합 S의 원소의 합이 K가 되는 S의 부분 집합을 찾는 문제이다.
[예제] S = {20, 30, 40, 80, 90}이고, 합이 200이 되는 부분 집합을 찾고자 할 때,
[해] {30, 80, 90}의 원소 합이 200이다.
Vertex-cover는 Subset-cover로 reduction
즉, Subset-cover이 더 어려운 문제
6. 0/1 Knapsack : 배낭의 용량이 C이고, n개의 물건의 각각의 무게와 가치가
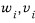 일 때 (단 i = 1, 2, …, n),
일 때 (단 i = 1, 2, …, n),
배낭에 담을 수 있는 물건의 최대 가치를 찾는 문제
Subset-sum은 knapsack으로 reduction
7. Hamiltonian-cycle : 주어진 그래프 G=(V,E)에서 임의의 한 점에서 출발하여
모든 다른 점들을 1번씩만 방문하고, 다시 시작점으로 돌아오는 경로를 찾는 문제이다.
Vertex-cover는 Hamiltonian cycle로 reduction
8. Traveling salesperson Tour : 주어진 가중치 그래프 G=(V,E)에서 임의의 한 점에서 출발하여
다른 모든 점들을 1번씩만 방문하고, 다시 시작점으로 돌아오는 경로 중에서
최단 경로를 찾는 문제
Hamiltonian-cycle은 TSP로 reduction
(선분의 가중치를 모두 동일하게 하여 여행자 문제의 해를 찾았을 때, 그 해가 바로 해밀토니안 사이클 문제의 해)
- NP-complete 문제들 중에 단 하나라도 polynomial time(다항 시간)안에 풀어낼 수 있다면 P=NP임을 증명할 수 있다.
왜? 모든 NP문제는 NP-complete 문제보다는 쉬움. NP complete를 푼다 -> NP모든 문제 푼다.
근데 NP complete를 다항시간에 푼다? 곧 P = NP
- NP complete 문제를 만나면 해결하려는 algorithm을 개발하는 것보다 approximation algorithm을 개발하는게 나을 것이다.
P = NP이냐 P != NP이냐는 아직까지도 증명 x
P = NP라고 증명이 된다면, 현재 NP라고 일컬어지는 모든 문제들이(길찾기, 방문 판매 알고리즘 등) 전부 P문제로서 풀릴 수 있다는 의미이다.
즉, 방문 판매 알고리즘 같이 시간이 오래걸리는 방법으로 풀 수 밖에 없다고 생각되는 것도 방법만 잘 찾는다면 다항 시간 내에 해결할 수 있다는 것이다.
반대로 생각해서 P != NP가 증명이 된다면, 수많은 NP 문제들이 P 문제로 환원될 수 없다고 증명됐으니 더 쉬운 방법(P 문제로 환원할 방법)을 찾으려고 애쓸 필요가 없다.
즉 이건 어려운 문제니까 쉬운 문제로 만드려고 해봤자 소용 없다는 걸 알게 되는 것이다.
